Week 3: Gradient Algorithms And Riparian Zones

Welcome back, everyone!

This week I continued working on my genetic algorithm, fine-tuning it, then started on a gradient-based algorithm. Gradient algorithms find the minimum of a function by calculating the gradient (slope) at the current point and then taking a step (of prescribed size) in the negative direction. If taking that step doesn’t lead to a lower value in the function at the new point, the step size is reduced until the new point has a lower value. Once around a local minimum, the code will often jump back and forth around the actual minimum value (see image below). The algorithm can also be used to find local maximums by following the gradient rather than going in the opposite direction.

As for my research, I continued reading others’ articles and noting the important findings. I learned it can be fairly easy for water to pass around the riparian zone, not through it, if, for example, a water table is right below the area and just out of reach for the plants’ roots. Water tables are a large concern for buffers’ efficacy in regions with shallow water tables. Also, depending on geography, certain riparian zones can be more important than others in an area. For example, in tidal areas, erosion due to waves and wakes is a large issue, and zone 1 (closest to the water) trees may actually add to bank destabilization when the rising sea level erodes the earth beneath them. Zone 1 trees must be carefully placed so they prevent, rather than add to, erosion along the riverbank. Until next week, Daria

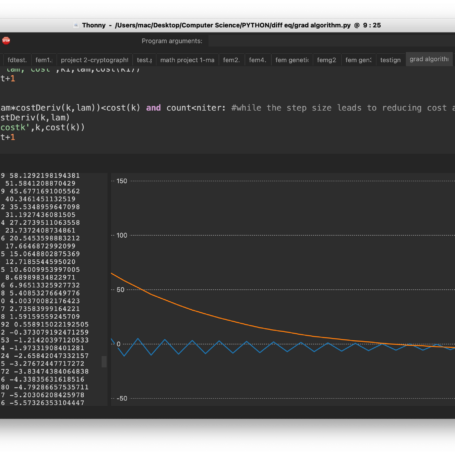
This is an example of my gradient algorithm. Note the oscillation of the blue line (chosen points) around a solution value (here, -3), while getting closer and closer to that solution. With more iterations, the oscillations won’t even be visible on the plotter. The orange line (cost, here x2+6x) is decreasing, but at a decreasing rate due to the decreasing step size (distance between points). The cost is decreasing towards its minimum, -9, but not oscillating.