Week 4: Latin Hypercube And SWAT

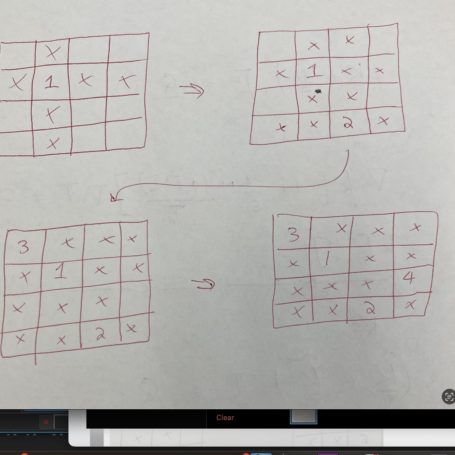
Hi, everyone! This week I continued improving my code for heat optimization, constraining the temperature to a certain value and adding terms to the equation I’m solving to essentially penalize (increase the cost function at that point) when the temperature exceeds this value. I had a lot of trouble with this, as the computed temperature would be above the value, then the penalty would bring it below the value, then there would be no penalty, so the temperature would go back to its original value above the value, etc., just oscillating. But eventually I got it to work, and now I’m working on coding Latin hypercube sampling. This is a program that randomly selects points that are spatially distributed to give a (probably) representative sample. The way this works in 2-D is that a point on, say, at 10×10 grid is selected, and the row and column that point is in are crossed out so no new points in that row or column can be chosen. Then a new point is chosen, its row and column crossed out, and so on (see image below). That way there is exactly one point in each row and column. This is useful, for example, when experiments are costly and you only have resources and time to run 10, but have 2 variables with 10 options each, meaning at 10×10 grid with 100 possible combinations. You want to choose 10 points (combinations of a value for each variable) that are distributed well to provide a meaningful representation of the sample and identify which regions should be examined in more depth. This idea can be extended into as many dimensions (variables, etc.) as you want.

As for my independent research, I want to first clarify ‘riparian buffers.’ These are regions of vegetation along riverbanks. Often, trees are right next to the water, with smaller plants (shrubs, then grasses) extending past the trees away from the river. I learned more about SWAT (Soil and Water Assessment Tool) and how much time and effort it takes to calibrate the program to get the coefficients right so the program can predict outcomes for new data. Automatic and semi-automatic calibration tools are available, and more are in development, increasing the accessibility of SWAT. Also, after calibrating the model, researchers then need to validate it. They calibrate the model on data from, say 5 years, then they take the next 5 years’ data and compare it to what the program predicts. This gives an estimate of how accurate the program is and shows when it over/underestimated values. This can be used to estimate the accuracy of that model over new data (i.e. proposed changes to the landscape that policy-makers want simulated before they are enacted).

I hope you learned something reading my blog post this week! No post next week, as I am on spring break, but see you the week after that. Daria