Last Week – A Crazy Finale

This week was a bit crazy… I spent the first half of the week finally testing the taxes, and the second half writing up my findings and finishing my presentation. It’s basically been a non-stop grind.

I started with Oskarssen’s rates of 15%, 25%, and 35% for income taxes, 1%, 2%, and 5% for wealth taxes, and 50%, 100%, and 500% for wealth taxes (Oskarssen 16). I decided to tweak these slightly to 0.15%, 1%, and 5% for wealth taxes because I found they produced easier-to-analyze results and covered a more broad range of taxes (also implemented in real life by some European countries). I also changed the 500% to 200% for land value taxes because 500% was such a massive outlier in the data that it was hard to present (literally obscured my graphs), and as Oskarssen notes, anything other than 100% is pretty arbitrary anyhow (but 200% is closer to real proposals and implementations).

I then analyzed my data with a made-up ratio of GDP/Gini Index, where higher values are better because they necessarily imply the tax caused either the economy’s productivity to decrease at a slower rate than equity increased, or the contrapositive. As you can see, this trend is broadly reflected in real life:

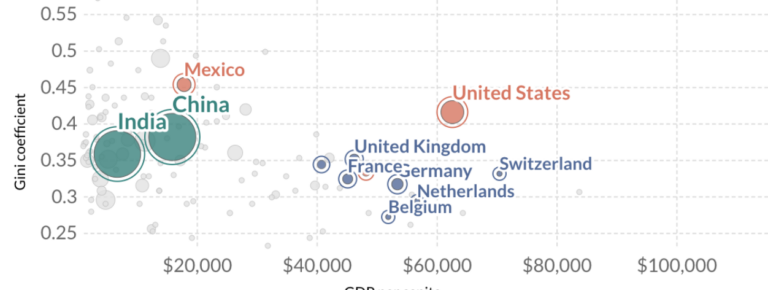
• In General, Almost All Taxes Were Neutral To Negative, As You Can See In The Chart Above. This Supports The General Assertion That Taxes Are Distortionary And Represent A Net-Negative Exchange For Society–An Idea Largely Backed By The Public Economics Literature (Røed 2). Though Taxes May Be Beneficial For Other Philosophical/Ethical Reasons, From A Purely Utilitarian Public Economics Perspective, Many Scholars Argue They Are Generally A Net Negative Beyond The Baseline Where Inequality Causes Market Inefficiency And Stunts Growth.
• The Specifics Of What Type Of Tax Works Best Aren’t Clear. In Broad Strokes, However, Land Value Taxes Were Least Optimal, And The Results Were Mixed Between Income And Wealth Taxes
• From The Standpoint Of Average Game Length, Which Can Be Viewed As Analogous To Keeping Players Above The Poverty Line, Since Games End At Bankruptcy, Lower Tax Rates Were Consistently Most Optimal, With Income Taxes Fairing Best, Followed Closely By Land Value Taxes And More Distantly By Wealth Taxes

IT Analysis

For income taxes, 25% was most optimal, with only a 0.44% decrease in GDP/Gini. All income taxes resulted in a less optimal outcome than baseline. As a result of the nature of the assumptions of this simulation (e.g. income sourcing), I would caution the reader not to use this data to conclude anything beyond that the relationship between optimality and the tax rate is nonlinear. All this definitely shows is, the relationship between income tax and optimality is clearly quite complex (as we would expect in real life), and while generally negative-to-neutral, it could even be more optimal than baseline at some untested value(s).

WT Analysis 

The wealth tax data was more complex. The variance in the data was comparatively quite small, making it more difficult to draw meaningful conclusions. It seems as if total tax revenue was generally weakly negatively related to optimality: the outcomes that we would expect to generate the most tax revenue (e.g. 5% at $1500, 5% at $2000) tended to be least optimal, and the outcomes that we would expect to generate the least tax revenue (0.15% at $2500, 1% at $2000) fared the best. Intuitively, this makes sense if we accept the general premise that wealth taxes are inherently distortionary. However, it’s worth noting there were many exceptions to this (we observe multiple instances of 0.15% taxes underperforming taxes that would be expected to generate more tax revenue). Also, some deviations from trends we would expect (e.g. higher tax rates decreasing Gini) may reflect imperfections of this simulation and/or indicate a more complex relationship between wealth taxation and income inequality. 

As a whole, the data does support the general assertion that wealth taxes are nonlinearly related to optimality and can be effectively targeted to the wealthy in efficient ways. We observed this directly with a 1% wealth tax at $2000, which produced a 0.1% more optimal outcome than the baseline. 

Theoretically, one wouldn’t expect to observe any incontrovertible difference between income taxes and wealth taxes, as they both disincentivize productivity in different ways (either through the investment of pre-existing wealth or time/productivity), which is in line with my findings.

LVT Analysis

The land value tax data was the most straightforward. Higher rates were less optimal. Theoretically, land value taxes are not very distortionary because they do not impact any inputs of productivity/investment in real life; however, in this simulation, the only investments that can happen (construction or purchasing properties) depend entirely on a player’s available finances and thus any distortions introduced would necessarily result from limiting their income. It’s worth noting that many of the real-life ​​benefits to LVTs, such as reducing over-speculation and urban sprawl, can therefore not adequately be simulated in Monopoly. This is a major limitation of my simulation.

Speaking of those, I’m also gonna text-dump the limitations of all this below:

Limitations

• People Obviously Don’t Always Behave Perfectly Rationally Or Homogenously, As They Did In This Simulation.
• Biases Towards The Short-Term And Loss Aversion Are Two Extremely Well-Studied Examples Of These That Would Be Present In Real Monopoly Players, But Are Not In My Simulated Agents (Haan 14).
• Random Variation Determines The Outcome Of Monopoly To An Arguably Disproportionate Extent
• Monopoly Is Probably An Especially Bad Vehicle For Testing Income Taxes Because Income Is Derived Entirely From Rent And Passing Go–In Other Words, Everyone’s Role Is Limited Exclusively To Landlord. This Is Problematic Because, At Least In The Short-Term, Effort Is Not An Input Into One’s Income In Monopoly–People Cannot Choose To Work Less Hard Or Fewer Hours In The Same Way They Might Be Able To In Real Life And Monopoly Players Can Cease Investing And Continue To Earn Income. Because These Real Distortionary Effects Of Income Taxes Are Not Reflected In My Simulation, My Results Are Likely Inherently Skewed
• The Only Significant Changing Variables In GDP Were I And G. Constructing Buildings, Buying Property, And Trade, Therefore, Accounted For All Distortions In The GDP Calculation (Government Spending Cannot Decrease), Which Simply Isn’t Reflective Of Reality. Because There Are Very Limited And Random Opportunities To Do Either In Monopoly, Investment Will Naturally Be Higher In More Unequal Games Because There Is A Baseline Threshold Of Money Required To Make Investments, And Once Those Opportunities Are Taken, Players With Excess Income Lower Than That Baseline Can No Longer Maker Investments, Whereas In Real Life, People Have All The Opportunities In The World To Invest (Or Spend) Their Additional Income. As A Result Of This, We Can Expect GDP To Be Higher In More Unequal Simulations, Which Will Inherently Bias My Project Toward Concluding Taxes Are Less Optimal.
• As You All Know (If You Read My Last Post), Trade Was Straight-Up A Mess And Not Particularly Reflective Of Reality Or Real Monopoly. The Idea We Can Use One Adjustment Factor Is Absurd (Park Place Is Probably Disproportionately More Valuable In Real Monopoly, For Example), But It Was A Necessary Oversimplification For Time/Ability Constraints.
• Having A Uniform Rate When Passing Go Made Sense For Simulation To Cap The Number Of Variables Being Tested At Once, But Government Social Welfare Spending Is Obviously Non-Uniform In Real Life.

Speaking of real life, it’s also worth mentioning that it’s not as simple as just implementing these different taxes: having the infrastructure to actually know the “highest and best use” value of land or someone’s total wealth is ridiculously complex. Tax avoidance also happens, distinguishing labor from capital can be difficult, and political factors like instability driven by inequality aren’t reflected here.

Speaking of real life, it’s also worth mentioning that it’s not as simple as just implementing these different taxes: having the infrastructure to actually know the “highest and best use” value of land or someone’s total wealth is ridiculously complex. Tax avoidance also happens, distinguishing labor from capital can be difficult, and political factors like instability driven by inequality aren’t reflected here. 

Points of Further Inquiry

• Heterogeneous Agents (Oskarssen 30).
• This Could Be Accomplished Through Modeling Degrees Of Risk Averseness And Intelligence Of Simulated Players In Monopoly, Which Is Honestly Beyond My Programming Capabilities,
• Or Through Testing These Parameters With Actual Players.
• Passing Go With Non-Uniform Redistributive Policies. One Could Conceivably Model Certain Policies, Such As Unemployment Checks Or Welfare, To Players Below An Income Or Wealth Threshold, Or Make Passing Go A Function Of One’s Wealth Or Income. In Theory, We Would Probably Expect This To Magnify The Impact Total Tax Revenue Has On The Simulation’s Results, Though It Could Meaningfully Attenuate Early Bankruptcies As Well.
• Unequal Starting Money And/Or Property Distribution (Stanley 347).
• Lastly, Incorporating Baur’s Housing Price Growth Into My Situation Would Be Much More Realistic, As It Would Open The Possibility Of Players Meaningfully Altering Their Wealth By Means Other Than Earning Income. This Could Make The Results Of Land Value Taxation And GDP (Through Adding Another Input) More Meaningful, And Would At The Very Least Bring The Results One Step Closer To Real Life.

Nathan out.