Week 4: Implementing a 3D EM Field Simulator

Hello and welcome back to my blog, where I’ll be tracking my progress on my EM field simulation project. Last week, I finished implementing the Yee algorithm in 1D and 2D. In addition to the obvious limitation of having less dimensions, our program also had various drawbacks such as lack of support for inhomogeneous media, crude boundary conditions, no support for lossy media (such as dielectrics), etc.

This week, I implemented the 3D Yee algorithm with a focus on adding greater functionality to our so-far simple simulation. This means that along with the challenge of translating our original simulation into 3D, I had to experience even more loss of sanity by implementing completely new concepts into our program.

Structuring the Program 

Not much thought was given into structuring the actual program with the 1D simulation due to its simplicity. The entire program was stored in one file and the entire simulation process was implemented in the Simulation class. Now, with the intent of adding more functionality to the simulation, I have to (unfortunately) structure the whole program with modularity, readability, and maintainability in mind. 

To make the program more modular, I’ve isolated the part of the program responsible for updating and storing the Yee grid. This way, I can implement complex features such as boundary conditions without having to change the constant part of the program.

Yee Grid in 3D

After giving some thought to the overall structure of the program, I started looking at the details for implementing the 3D Yee grid. As I’ve mentioned, the Yee algorithm discretizes the EM fields by storing them in a staggered grid, with some fields being stored at half-steps in space. Having implemented the staggered grid before, all I had to do was generalize it to 3D. The 3D simulation now has to calculate all 3 components of both fields. The arrangement of the fields on the Yee cell is shown below, with the electric fields on the midpoints of the edges of the cell and the magnetic field components on the faces.

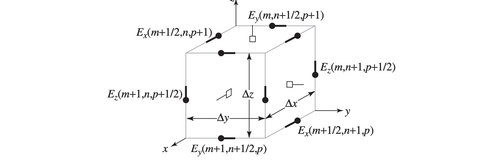
The update equations for the program remain the same, just generalized to 3D (there’s also more of them because we now have 6 field components to update). Once again, the equations are derived by discretizing Ampere’s and Faraday’s Laws.

ABC (Absorbing Boundary Conditions)

In order to avoid having our fields reflect back at the boundaries, we must have a boundary condition that completely absorbs the field. This way, the simulation appears to be surrounded by infinite space.

There are several types of ABCs, and I chose to implement a first-order ABC based on the Advection Equations (shown below):

A solution to either advection equation is also a solution to the wave equation, which dictates how an electric/magnetic field propagates in free space. Essentially, the ABC works by using the advection equation to predict the behavior of the fields near the boundary in order to calculate the values needed at the boundary to absorb the incoming field. Once again, the calculation is performed by discretizing the differential equation.

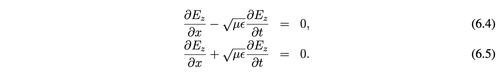
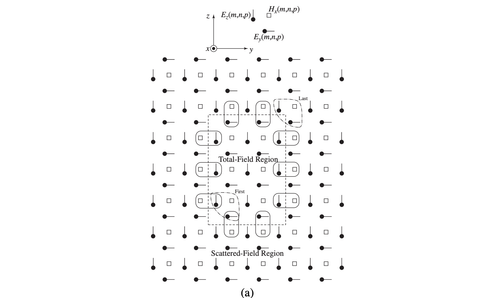
TFSF (Total Field Scattered Field) Boundary

Another kind of boundary condition I implemented was the TFSF boundary. The purpose of this boundary condition is to allow the presence of an incident field within a restricted area of the simulation. The TFSF boundary is implemented by dividing the total simulation area into two regions, the total field region and the scattered field region. In the total field region, an incident field term is added to the update equations to simulate the presence of a source. The incident term can be calculated analytically, but in some cases, a subsidiary Yee algorithm can be used to track the evolution of the incident term before plugging it into the main algorithm.

Conclusion

Thanks for reading the whole thing! In the next week, I will finish up my implementation and show some EM field simulations in 2D and 3D. Stay tuned for the results!

Sources:

https://eecs.wsu.edu/~schneidj/ufdtd/

https://github.com/flaport/fdtd?tab=readme-ov-file