Week 1 | Standard Economic Theory Is Flawed!
March 10, 2023
Hi readers!! I’m so excited to be taking you all through this journey with my Senior Project. For the next several weeks, I’ll be detailing my findings and progress here on this blog. By the end of these 12 weeks, I hope to have designed and conducted my own economic game. For this first post though, let’s start off by playing a simple economic game 😀
The Prisoner’s Dilemma
A classic. Most likely you know or have heard about this game before. Essentially, two prisoners are both given two choices: confess or stay silent. If both confess, both prisoners get 5 years in jail. If both stay silent, both prisoners get 2 years in jail. However, if one confesses and one stays silent, the one who confesses gets let off while the one who stays silent serves 10 years. (This is just one variation of the game; you might have seen it with different numbers involved).
To illustrate this in game theory, we utilize a payoff matrix, as shown below:
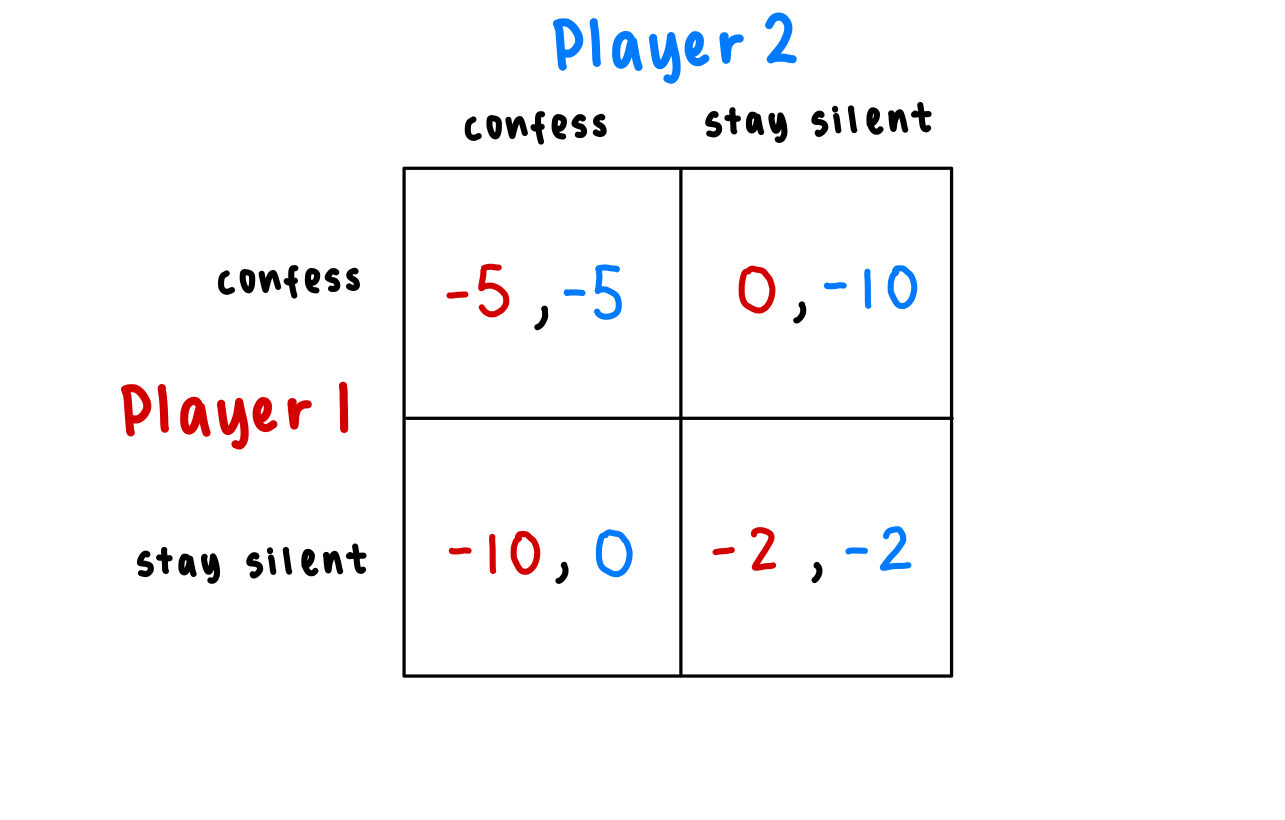
I color coded it so it’s easier to understand. Red corresponds to the payoffs for player 1, and blue corresponds to the payoffs for player 2. Each square corresponds to a set of strategies.
If you were one of the players, what would you choose? Confess or stay silent?
Intuitively, we might think: well, isn’t the outcome better for everyone if both just stayed silent?
Wrong. Well, it’s wrong according to standard economic theory at least, which assumes that perfectly rational decision makers are selfish, only looking out for their own best interests. Thus, it is in each player’s best interest to confess since that yields the highest payoff for him/herself regardless of what the other player chooses.
Nash Equilibrium
This static state of {confess, confess} where neither player has an incentive to change his or her playing strategy is known as the Nash equilibrium (termed after John Nash). For the purposes of behavioral economic research, Nash equilibrium is incredibly important as it can serve as a predictor of theoretical and rational behavior.
However, it has been observed in many economic games that real-life human behavior often does not align with these predictions from Nash (hence why standard economic theory is flawed!!), and I plan on exploring more instances of this through my project.
Behavioral Economics
The prisoner’s dilemma game is a classic example of strategic decision making where the predicted rational outcome ({confess, confess}) is not the socially optimal outcome ({stay silent, stay silent}). These deviations from standard economic theory led to contributions in the field of behavioral economics, which utilizes social preferences and utilities to explain why human behavior isn’t rational at times.
What does that have to do with my project?
As for my project, I’ll be specifically looking at how acts of generosity and vulnerability may influence people’s levels of cooperation. By designing my own game with a clear Nash equilibrium (I’m thinking a one-shot, two-stage game at the moment, but anything is up to change!), I’ll be able to study people’s deviations from Nash to see whether generosity and vulnerability actually influence people to be more cooperative. Perhaps my results can inform businesses about how they can better develop sales and marketing strategies to connect with their customers!
I hope to spend the next few weeks studying several economic game designs and behavioral economics concepts before delving into my own game.
I’m also planning on using Prolific to distribute my game and recruit participants. The online platform is fairly easy to use, and I can even distribute monetary bonuses on there.
I hope you enjoyed this tiny glimpse into game theory, behavioral economics, and my senior project! I’ll try to include a fun game for each blog that I post 😀
Until next time,
Cindy
Sources
Rabin, M. (1998). Psychology and Economics. Journal of Economic Literature, 36(1), 11–46. http://www.jstor.org/stable/2564950
Goeree, Jacob, K., and Charles A. Holt. 2001. “Ten Little Treasures of Game Theory and Ten Intuitive Contradictions.” American Economic Review, 91 (5): 1402-1422.
Holt, C. A., & Roth, A. E. (2004). The Nash equilibrium: A perspective. Proceedings of the National Academy of Sciences, 101(12), 3999–4002. https://doi.org/10.1073/pnas.0308738101
