Week 11: Semidirect Products of Cyclic Groups

Welcome back! I’ve found many working groups, most of which are the semidirect product of two cyclic groups. Today, I’ll discuss what this means and how we can check if they work.

The Cyclic Group C_n

I haven’t discussed cyclic groups in detail yet. They are essentially the group of rotations of a regular polygon with n sides. There are two other ways to think about this. One is that they are the groups of integers under addition, with everything taken as a remainder when divided by n. The other is that it is generated by one element a with aⁿ = e (where e is the identity).

Semidirect Products G ⋊ H

I’ve discussed the semidirect product before, so I’ll quickly review that now. An automorphism is a homomorphism from G to itself, i.e. a map φ: G -> G where φ(gg’) = φ(g)φ(g). Let’s consider a homomorphism from H to the automorphism group of G. This is a collection of maps φ_h: G -> G where φ_hh’ equals the composition φ_h • φ_h’.

Then, the semidirect product is the set of ordered pairs (g,h) where g and h are elements of G and H, respectively. Multiplication is given by (g,h)•(g’,h’) = (gφ_h(g’), hh’).

Possible φ for Cyclic Groups

Let’s now consider the case when G is the cyclic group C_n, and H is the cyclic group C_m.

Automorphisms of cyclic groups are relatively easy to determine. Any homomorphism is determined from how it acts on generators, and cyclic groups only have one generator. Then the automorphism is uniquely defined by φ(a). As long as this is an order n element, we get a valid automorphism. Then these are given by φ(a) = a^k, where k is relatively prime to n. 

Let b be the generator of H. Then φ_b(a) = a^k for some k. Ideally, k is not 1 — otherwise, this is a trivial homomorphism and just gives us the normal direct product.

Now, because b^m is the identity, φ_b^m(a) = a. Because it’s a homomorphism, this also equals a^{(k^m)}. Then, k^m should leave a remainder of 1 when divided by n.

Because we are working with modular arithmetic, we first focus on when n is a prime. A classic result from number theory is that if m and n-1 are relatively prime, then 1 is the only possibility with n | k^m-1. Therefore, we can only consider primes n such that n-1 shares a factor with m.

What Do We Want?

By now, we have a sufficient understanding of what the semidirect product of cyclic groups is. But why did I think that they’re especially nice to consider?

In my Week 8 post, I mentioned that a key characteristic of the dicyclic group is its “sign representation”. In particular, it’s generated by two elements a and b, and we can take a representation that only considers the component of b. Among the conjugacy classes, very few actually have a component of b. In fact, only two of the n-3 conjugacy classes differ from the trivial representation here. This was key to the argument I discussed for the dicyclic groups, as well as the argument Naidu and Rowell used for dihedral groups.

The reason we can take this sign representation is because if we imagine splitting the generators a and b into two components, as in the definition of the semidirect product, then the multiplication of the second components is identical to that of a cyclic group. This property is shared by semidirect products of cyclic groups in general.

Therefore, we will have some one-dimensional representations. These assign all group elements (g, e) to 1.

To elaborate on the properties I want, it’s probably easiest to demonstrate some working examples.

The Groups I’ve Found

Before I show the groups, I’ll quickly re-explain how to determine the multiplication rules of the irreducible representations. Let χ_i be the character corresponding to V_i. Then, V_i ⊗ V_j = Σ (χ_iχ_j • χ_k) V_k.

In particular, V_i ⊗ V_j = V_j exactly when for all conjugacy classes (represented by some g), χ_i(g)χ_j(g) = χ_j(g). This is true when either χ_i(g) = 1 or χ_j(g) = 0.

C₁₃ ⋊ C₃

Now, let’s look at the character table of C₁₃ ⋊ C₃. The homomorphism is φ_b(a) = a⁹ (note that 9³-1 = 728 = 13•56). All character tables are taken from [1].

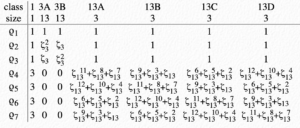
That may look complicated, especially because the bottom-right 4×4 square of entries is quite messy.

Firstly, ζ denotes the roots of unity, so ζ₃ is a complex number with ζ₃³ = 1, and similar for ζ₁₃. The terms involving the latter are not easy to work with. However, if we look more closely at the one-dimensional representations, they indeed have the property I mentioned earlier: in every column, either they give 1, or all the other characters give zero.

Let V denote the the representation corresponding to the second row. Then for any of the three-dimensional representations, V ⊗ X = X. Take the algebra A = 1 ⊕ V ⊕ V². By following the same argument as in the dicyclic case, in the category of A-bimodules, the four three-dimensional representations each are irreducible objects with nine unique structures each. The other simple objects combine for a Frobenius-Perron dimension of 3, and since the category is integral, they must all be invertible too.

C₁₁ ⋊ C₅

Let’s look at another example. Now, the homomorphism is φ_b(a) = a³. 

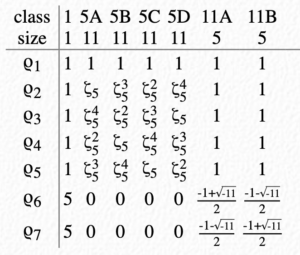
Again, in each column, either the one-dimensional representations give 1 or everything else gives 0. Therefore, if A is the direct sum of the one-dimensional irreducible representations, then in the category of A-bimodules, the final two representations are simple objects, with 25 structures each. Then, the remaining simple objects account for a Frobenius-Perron dimension of five.

It is now possible that we have a two-dimensional simple object, so we need to do some more work here. However, the key property of these character tables has reduced the problem into a much simpler one, and one which we can directly tackle.

Some other character tables

For now, I’m focusing on the semidirect product of two cyclic groups. However, I’ve encountered many other examples of character tables which fit my desired archetype.

One is the character table of C₃⋊D₃:

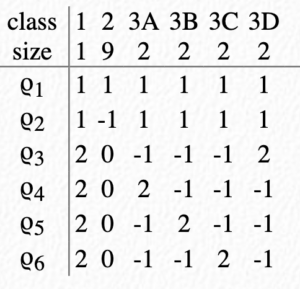
Recall that D₃ is a dihedral group, which we know also has simple conjugacy classes and a sign representation.

Another example is C₃²⋊C₄:

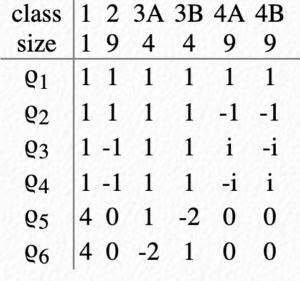
I’ll quickly discuss what the first group in the product is, because while it isn’t related to today’s blog, it’s a very logical next direction. The exponent denotes the direct product, so C₃² is the group of ordered pairs (a,b), where each component has independent multiplication by the C₃ rules. To describe it with presentations, it’s generated by elements a and b with a³ = b³ = 1 and ab = ba.

The second condition makes the group commutative. In fact, the Fundamental Theorem of Abelian Groups says that any finite, commutative group is the direct product of some cyclic groups. The Chinese Remainder Theorem, a basic number theory result, lets us strengthen that: each of the cyclic groups has an order that is a prime power.

Direct products are structurally really simple — they just separately have the structures of their two components. Therefore, Abelian groups in general are a reasonable next step to take.

Anyway, that’s for the future. For now, we just want to understand the structure of semidirect products of Abelian groups.

Conjugacy classes of C_n⋊C_m

I’ll first give an exact characterization of the structure of the group. The simplest way to do this is with group presentations. However, we must first address a number theoretical question.

The choice of k

For convenience, we denote the generators of each of the cyclic groups by 1. Suppose our homomorphism is given by φ₁(1) = 1^k. (Here, since the operation is addition, 1^k is the result of adding 1 to itself k times, which is just k.)

As before, k^m-1 must be a multiple of n. Since we’re now considering multiplication modulo n, we restrict our attention to when n is a prime. Then, it’s guaranteed that we can choose some k other than 1 such that k^m-1 is a multiple of n.

However, this choice might not always be ideal. For example, if m=4 and k=n-1, then k²-1 is a multiple of n, so we don’t get as much freedom as we might want.

Thankfully, a standard result from number theory gives a satisfying answer. Let m’ = gcd(m, n-1), which we assumed is greater than 1. Then, we can pick a k such that m’ is the smallest exponent where k^m’-1 is a multiple of n. Furthermore, all other such exponents are multiples of m’.

This result has a fun proof, but I’ll omit it for the sake of space. If you’re interested, please feel free to ask! For now, one more assumption simplifies our work a lot: we assume that m is a factor of n-1. Then, m’ is just m, and we pick some k as discussed above.

The group presentation

Let a = (1,0) and b = (0,1). Then a and b generate the semidirect product, and aⁿ = b^m = 1. Moreover, based on the multiplication rules of a semidirect product, we have ab^-1 = (1,-1) and b(ab^-1) = (φ₁(1), 0) = (k, 0) = a^k.

Now we have our three rules. I’ll rewrite these together for clarity: aⁿ = b^m = 1 and bab^-1 = a^k. It’s often helpful to rewrite the last one as ba=a^kb.

An important property that I’ve hinted at before, which is why we can consider the sign representation, is that the power of b is “invariant.” This isn’t a rigorous term, but essentially, to get the power of b in any multiplication, we can just ignore all the a‘s. We’ll see why exactly this is more important once we are ready to characterize some of the representations.

Multiplication rules

We now have characterized the group, but it’s usually helpful to derive some more multiplication rules to simplify calculations.

First, we can compute ba² = (ba)a = (a^kb)a = a^k(ba) = a^k(a^kb) = a^2kb. We can inductively generalize this to ba^c = a^ckb. (If you’re interested, this can be a quick exercise.)

Now, we have b²a^c = b(ba^c) = b(a^ckb) = (ba^ck)b = (a^ckkb)b = a^ckkb². Again, we can inductively generalize this to b^da^c = a^{ck^d}b^d.

Let’s quickly check that this is sensible. We know that b^m=e, so b^ma^c should equal a^cb^m. Indeed, the ratio between these is a^{c(k^m-1)}, and as I showed earlier, k^m-1 is a multiple of n, so a^{c(k^m-1)} = e.

Describing the conjugacy classes (part 1)

Again, we’ll focus on the case when n is a prime, and this implies that n-1 shares a common factor with m.

For some element g, the members of its conjugacy class can be expressed as hgh^-1 for some h. Let g=a^cb^d, and let h=a^eb^f. Then h^-1=b^-fa^-e.

First, we have hg = a^eb^fa^cb^d = a^{e+ck^f}b^f+d. Then, hgh^-1 = a^{e+ck^f}b^f+db^-fa^-e = a^{e+ck^f}b^da^-e = a^{ck^f+e-ek^d}b^d.

As I’ve mentioned before, we can observe that any two elements in the same conjugacy class have the same exponent of b. Picking some arbitrary f, the exponent of a is ck^f-(k^d-1)e. Another common fact in number theory is that any equation of this form, where k^d-1 shares no factors with n, achieves all possible residues modulo n. (The main idea is that by Bezout’s Lemma, k^d-1 has a multiplicative inverse modulo n). Anyway, because we reach all possible residues modulo n, any two terms a^cb^d and a^c’b^d are in the same conjugacy class (when d is nonzero). In other words, the only condition is that they have the same, nonzero exponent of b.

The d=0 case is a bit different, because for some a^c, the elements in its conjugacy class are of the form a^{ck^f}. To fully describe these classes, I’ll introduce another idea from group theory.

Cosets

For a group G, a subgroup is any subset H which is “closed under multiplication”. Specifically, for any h and h’ in H, their product h•h’ should also be in H.

For an element g, let gH denote the set of elements that can be expressed as gh for some h in H. The main idea is that if we write out gH for each g, any two overlapping cosets are the same. Additionally, each coset has the same size, which is the size of H. The proof of this is quite elegant, but my post is already slightly long so I’ll omit it.

Therefore, if there are x unique cosets, then since these exactly partition the full group G, we have x|H|=|G|.

Describing the conjugacy classes (part 2)

When we think about cosets, the main group G is the multiplicative group modulo n. To be precise, it contains of the elements 1, 2, …, n-1, and its operation is multiplication, followed by taking the remainder when divided by n. The subgroup H is generated by k, so it contains the powers of k. Since k^m=1, and since m is the smallest such exponent, H as m elements. The conjugacy classes of elements a^c are exactly described by cosets, and because G has n-1 elements, there are (n-1)/m of these.

In summary, we have one conjugacy class for each of the m-1 nonzero exponents of b. We have (n-1)/m conjugacy classes for powers of a. We also have one final class, which only consists of the identity (which we can just call 1).

The one-dimensional representations

We’ve already done most of the work to describe the one-dimensional representations.

Recall that the commutators are elements of the form ghg^-1h^-1. If we generate these as h=a^cb^d and g=a^eb^f, then we already computed that ghg^-1 = a^{ck^f+e-ek^d}b^d. Since h^-1=b^-da^-c, we have ghg^-1h^-1 = a^{c(k^f-1)-e(k^d-1)}. By similar logic as before, if we arbitrarily pick c, f, and some nonzero d, then by varying e, we achieve all powers of a. Then there are n commutators (the powers of a, since aⁿ=1).

As I mentioned in my Week 6 post, the number of one-dimensional representations is the size of the group divided by the number of commutators. The former is mn, so there are m one-dimensional representations.

When describing a representation, we only need to define how it acts on the generators. As I’ve mentioned before, these resemble the “sign representations” in that they entirely neglect components of a. To formalize this, if we call the representation ψ, then ψ(a)=1.

We still need the other two relations from the presentation: ψ(b)^m=1 and ψ(b)ψ(a)ψ(b)^-1=ψ(a)^k. The latter is automatic, because we can ignore the a terms and the rest cancel. The first tells us that ψ(b) can be any complex m-th root of unity.

There are m such roots of unity, so there are m one-dimensional representations that neglect a. In fact, this matches the total number of one-dimensional representations, so we’ve fully characterized them!

The other representations

First, let’s find the dimensions of these representations! As I discussed in my Week 6 post, the sum of the squares of each irreducible representation’s dimension is the size of the group, which is mn. Also, the number of irreducible representations is the number of conjugacy classes, which is m+(n-1)/m.

We already have m one-dimensional representations, so there are (n-1)/m remaining representations, and the sum of the squares of their dimensions is m(n-1).

You may immediately guess that all remaining representations therefore have dimension m. This does hold in all relevant character tables I found online! However, it’s not so easy to show, and we don’t need it just yet. It still seems like a fun exercise, so I might try it later. A possibly important idea is that the conjugacy classes given by cosets are basically indistinguishable, so we can try to “clone” a working representation.

While I haven’t yet figured out how to prove this, I did succeed in proving the main condition.

Checking the key property

The original reason I noticed these groups are nice to consider is because of the property I mentioned earlier: that in each column, either the one-dimensional characters all give 1, or everything else gives 0. Here, I’ll prove that our semidirect product satisfies this property.

Let the one-dimensional characters be 1, χ, χ², …, χ^m-1. The representatives of the relevant conjugacy classes are just powers of b, so if χ(b)=ζ, then χ^c(b^d)=ζ^cd.

The critical idea is that the sum Σ ζ^-idχⁱ is m for b^d, and zero for everything else. This is a fairly standard computation with roots of unity; again, I’ll omit it due to this post already being just a bit too long.

Given this fact, because χ’ • χⁱ = 0 for any multi-dimensional character χ’ and integer i between 1 and m-1, by linearity χ’ • Σ ζ^-idχⁱ = 0. Therefore, χ'(bⁱ) = 0, as desired.

Conclusion/Summary

That was a really long post, so I’ll take some more time to summarize it. The main update is that I’ve found a few new groups that answer my research question. I discussed why these work, and I also looked quite deeply at the general case. Specifically, I described the structure of the semidirect product of C_n and C_m, where n is a prime and m is a factor of n-1. I classified the conjugacy classes, and determined a few key properties of the character tables.

This isn’t yet enough to fully prove the general case (although it does suffice when m=3). However, the remaining work seems quite similar to proving that Abelian groups satisfy the research question, so I expect that these will all work.

Finally, there are a few ways in which we can further generalize this case. I’m not sure if they’ll succumb to a similar argument, but at least we can determine the conjugacy class composition. I didn’t include them in this post because it’s already long enough, but they might be promising future directions.

References

https://people.maths.bris.ac.uk/~matyd/GroupNames/characters.html